Prepare-se para se divertir com a nossa dose desafiadora de passatempos matemáticos preparados exclusivamente para você !
Números são belos por natureza. Um cálculo bem elaborado tem a elegância e a precisão de uma bailarina. Tente solucionar estes passatempos matemáticos e veja se você consegue ouvir a orquestra.
Intrusa peso leve
Pagando uma revista com uma nota de 10 reais, recebi nove moedas de 1 real de troco. Logo depois, o jornaleiro me telefonou para dizer que uma das moedas era falsa e que, exceto por ser ligeiramente mais leve, seria indistinguível de uma moeda verdadeira.
Qual é o número mínimo de pesagens necessárias, usando uma balança de dois pratos, para localizar a moeda falsificada?
Rolem os dados
Uma conta foi feita com as faces superiores de três dados, mas ela não faz sentido.

Para torná-la correta, você deve rolar cada dado em qualquer direção em um quarto de volta. Quantas soluções existem e quais são elas?
Terapia a varejo
Uma consumidora comprou um único item de cada uma das três barracas que visitou numa feira. Em cada barraca ela gastou 2⁄3 do que tinha e, no fim, ainda ficou com 50 centavos de sobra para a passagem. Quanto ela possuía no início?
Maldito sistema monetário
– Graças a Deus! – exclamou a Srta. Juliana ao caixa assim que descontou seu cheque.
– Ao ler meu cheque, devo ter trocado os centavos pelos reais e os reais pelos centavos, moço. Eu nunca lidei muito bem com o sistema monetário. Tenho o dobro do dinheiro que imaginava.
– Para ser perfeitamente preciso, senhorita – respondeu o caixa –, se a senhorita gastar dois centavos do que realmente tinha, ficará com exatamente o dobro do que imaginava ter. Inicialmente, de quanto era o cheque?
O problema do guarda-chuva
Qual é o número representado por x neste guarda-chuva?
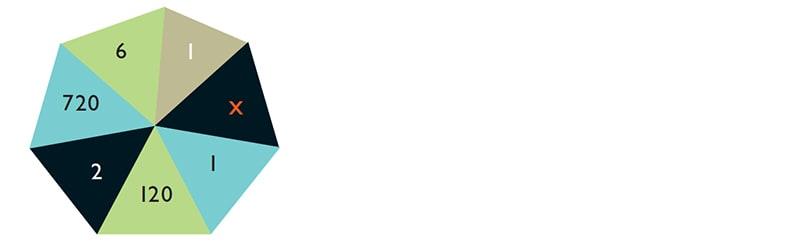
Respostas:
Intrusa peso leve
Duas pesagens resolvem o problema. Ponha três moedas em cada um dos pratos. Se elas não ficarem em equilíbrio, pegue duas do lado mais leve e pese-as. A moeda mais leve é a falsa. Se a balança ficar em equilíbrio, a terceira moeda é a falsa. Suponhamos que as três moedas de cada lado fiquem em equilíbrio. Prossiga então com as três moedas restantes do modo descrito acima.
Rolem os dados
Tome o primeiro dado, o da face 6, por exemplo. Como faces opostas sempre somam 7, sabemos que 1 está na face oposta ao 6. Portanto, os quatro números que estão a um quarto de volta de 6 são 2, 3, 4 e 5. O mesmo acontece com os outros dados. Portanto, as opções são: (2, 3, 4 ou 5) x (1, 2, 5 ou 6) – (1, 3, 4 ou 6) = 11. Considerando uma combinação por vez, descobrimos que existem duas soluções:
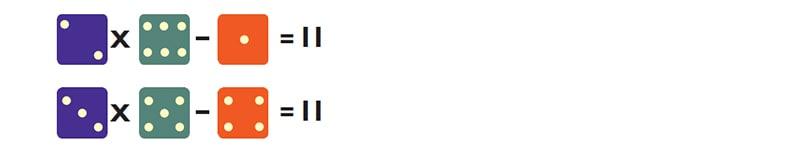
Terapia a varejo
R$ 13,50. Após cada transação, a consumidora fica com um terço do que tinha antes. Assim, o que tinha antes de uma transação é três vezes o que tinha depois dela. Resolvendo de trás para a frente, ela deve ter começado com 3 x 3 x 3 x 0,50 = 27 x 0,50 = 13,50.
Maldito sistema monetário
O cheque era de R$ 65,32. A Srta. Juliana confundiu o 32 com o 65 e esperava R$ 32,65. Ela recebeu R$ 65,32. Se gastar dois centavos, ela terá R$ 65,30 – que é exatamente o dobro de R$ 32,65.
O problema do guarda-chuva
x = 24. Comece pelo 1 na parte superior direita e, percorrendo no sentido horário, pule para segmentos alternados, multiplicando por 1, 2, 3, 4, 5, 6 de modo a desvendar a sequência 1, 1, 2, 6, 24, 120, 720.
Clique aqui e confira mais alguns jogos!